NAEP Results on Writing Decimals as Fractions

FOURTH MATHEMATICS ASSESSMENT

National Assessment of Educational Progress c. 1989

About three-fourths of the 11th-grade students could locate a decimal on the number line which is comparable to the number of students who could locate a common fraction on the number line.

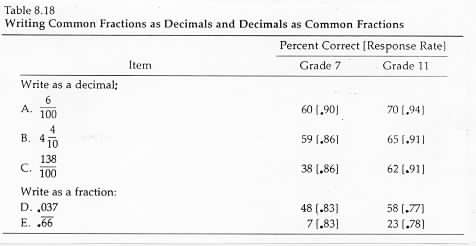
The results for the items that assessed students’ ability to write common fractions as decimals and decimals as common fractions are summarized in table 8.18. About 60 percent of the 7th-grade students and 65-70 percent of the 11th-grade students could express simple fractions as decimals. The 7th-grade students’ performance was significantly lower for the item that involved an improper fraction. Students in grade 11 had less difficulty with this item. For both groups performance was lower on the item that involved changing a decimal to a common fraction even though the fraction did not have to be reduced. This was the only item that involved thousandths which may account for part of the difficulty. But it would be inappropriate to conclude on the basis of a single item that students have greater difficulty with decimals beyond hundredths. At both grade levels students were generally unfamiliar with common repeating decimals.

The results for the items involving the comparison of decimals are summarized in table 8.19. For 7th-grade students performance on these items was significantly below their performance on the items that involved writing decimals as fractions; for 11th-grade students performance was actually somewhat higher.

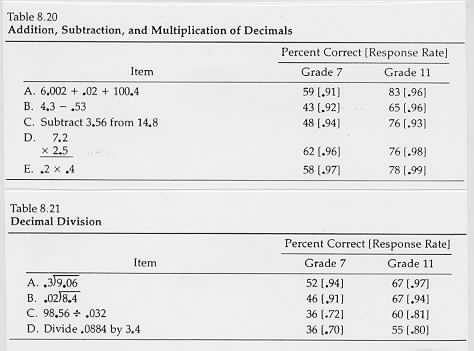
Results for the decimal-computation items are summarized below in tables 8.20 and 8.21. Students in grade 7 were more successful adding and multiplying than subtracting or dividing. For the 11th-grade students performance was more consistent over the four operations.

Every division item had zeros in the quotient so the computations were relatively difficult. Given the range of subskills required in the division problems performance was relatively consistent over the four problems particularly in the 11th grade. The results suggest that most students who have learned to divide decimals have learned the broad range of subskills necessary to solve different types of problems but about a third of the 11th grade students have learned very little about dividing decimals and cannot solve the most basic decimal items.

The results for the items involving calculations with percents are summarized in table 8.23. The results for the two items in which students were asked to find what percent one number is of another number suggest that students are significantly more successful working with familiar percents like 50 percent that they are with less frequently encountered percents like 7 percent. They seem to be able to solve simple problems involving familiar percentages for which they know fraction equivalents without relying on computational procedures.

Not surprisingly students were more successful calculating a percent of a number than solving other types of percent problems. Their overall success in calculating the percent of a number was about equivalent to their success in expressing percents as decimals and decimals as percents.

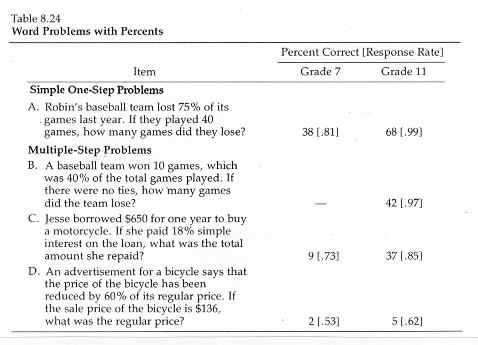
Results for selected word problems containing percents are summarized in table 8.24. Students were about as successful in solving simple one-step word problems as they were in performing similar calculations; however many multiple-step word problems were much more difficult even when the additional step required relatively simple arithmetic. Although item B requires several steps to find the total number of games played and then to subtract the number won to find the number lost the extra step is relatively obvious and performance on this item was at about the same level as performance on corresponding calculation items (see item E in table 8.23).

Item C however was much more difficult than item A even though they both required

computing a percent of a number. Although the problem involving the repayment of a loan may not appear to require any great insights about high finance it appears that many students treated the problem rather mechanically without thinking about the fact that the repayment should include both the principal and the interest. It is possible that many students did not think about the problem as a real-world situation.
The last problem involved several steps along with a relatively difficult calculation. It also required some attention to the problem situation to recognize that the price had been reduced 60 percent not that the sale price was 60 percent of the regular price. This problem was extremely difficult for almost all students.
It would be inappropriate to conclude from the results of items C and D that performance would be the same if students were in a real situation in which they needed to perform similar calculations but it appears that many students may treat word problems they encounter in school and on tests without thinking about the situation they represent.